Your Paper Summary

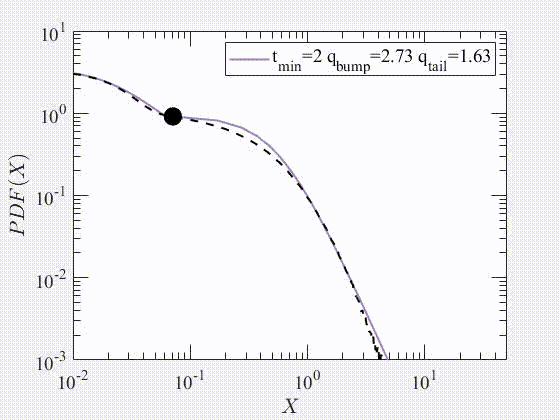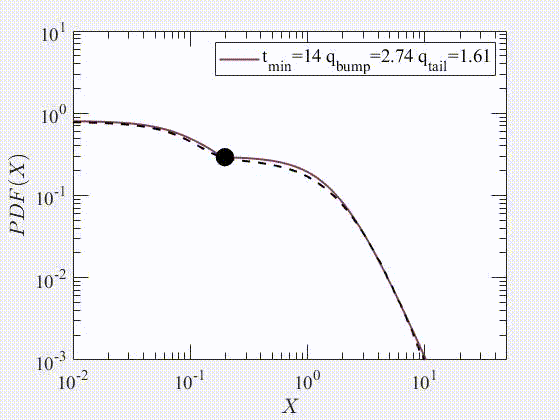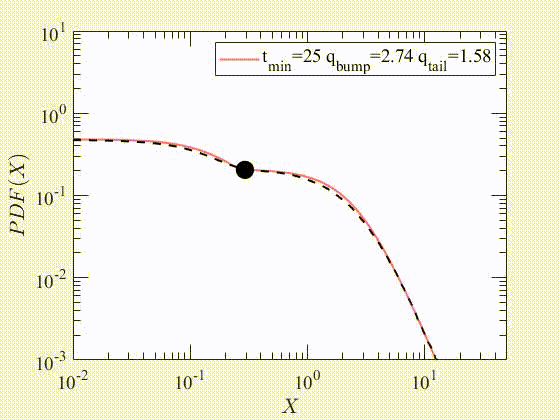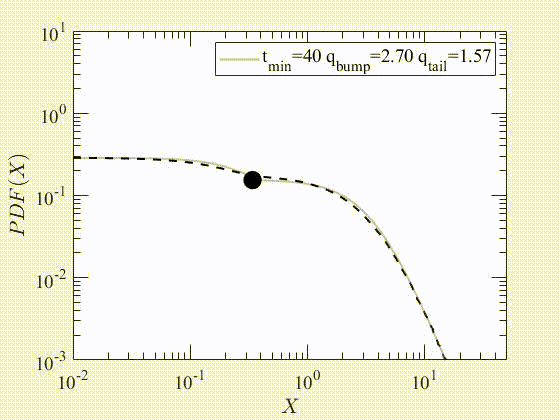
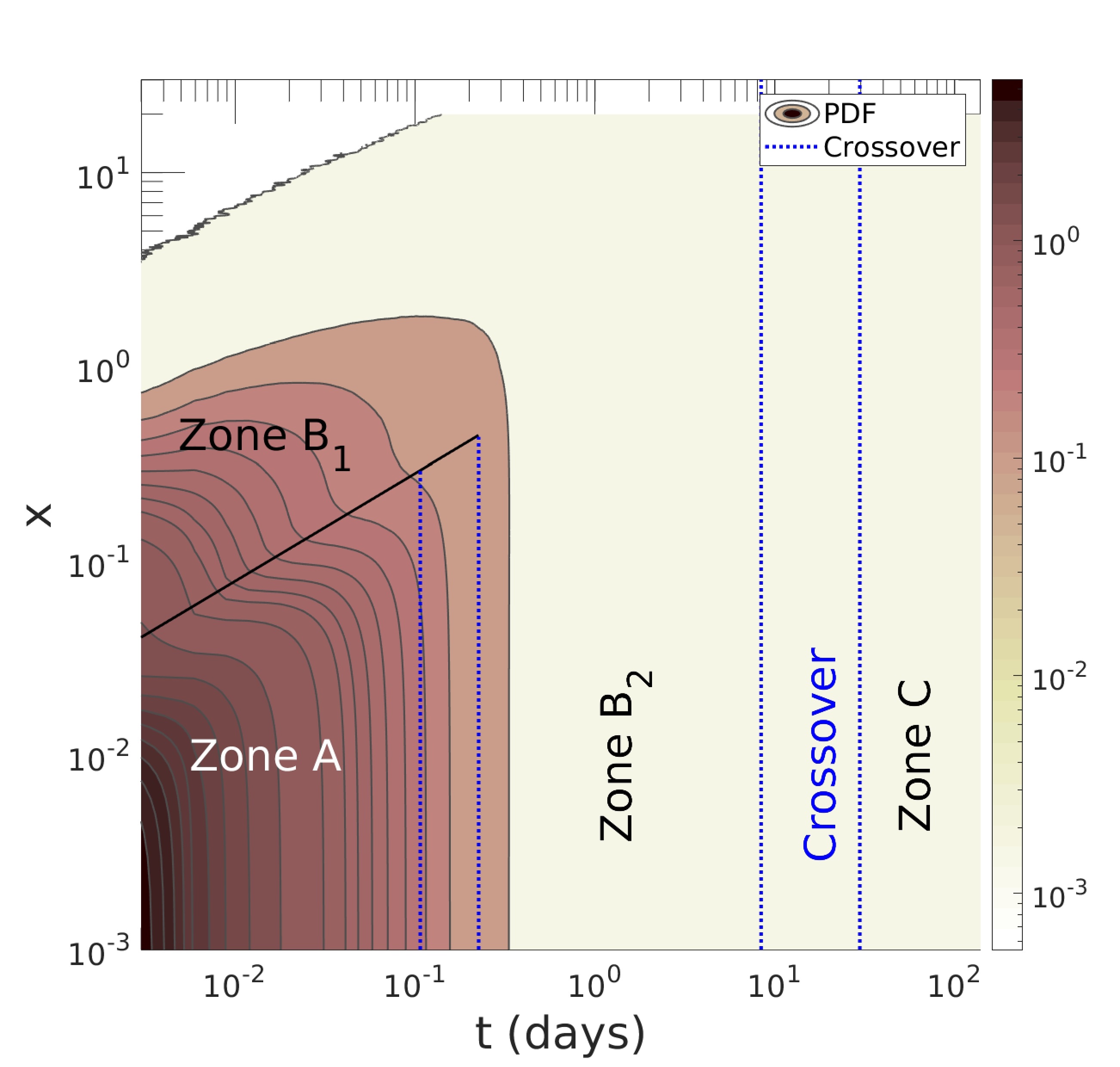
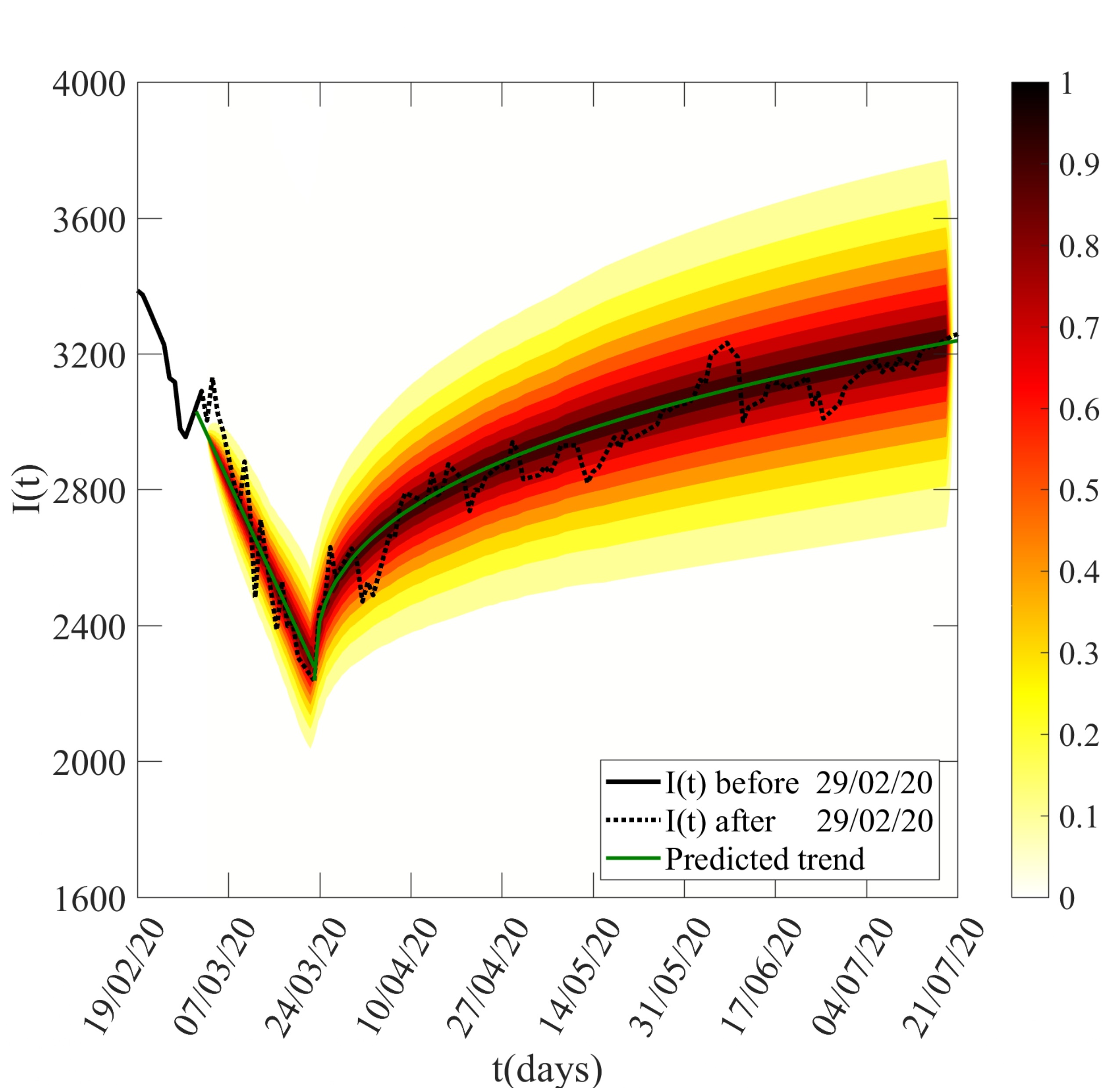
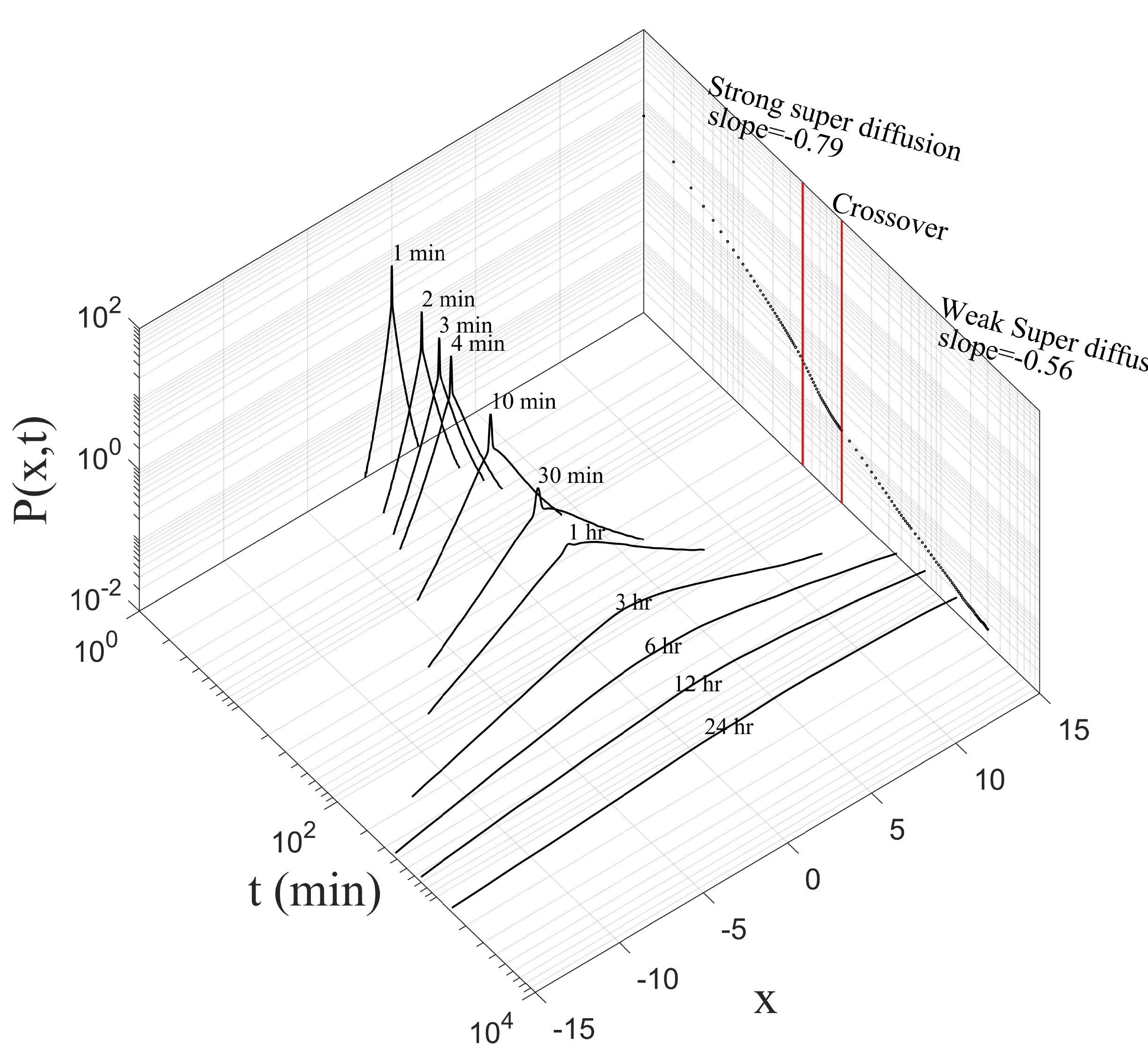
2022 Testing stationarity of the detrended price return in stock markets

(click here)

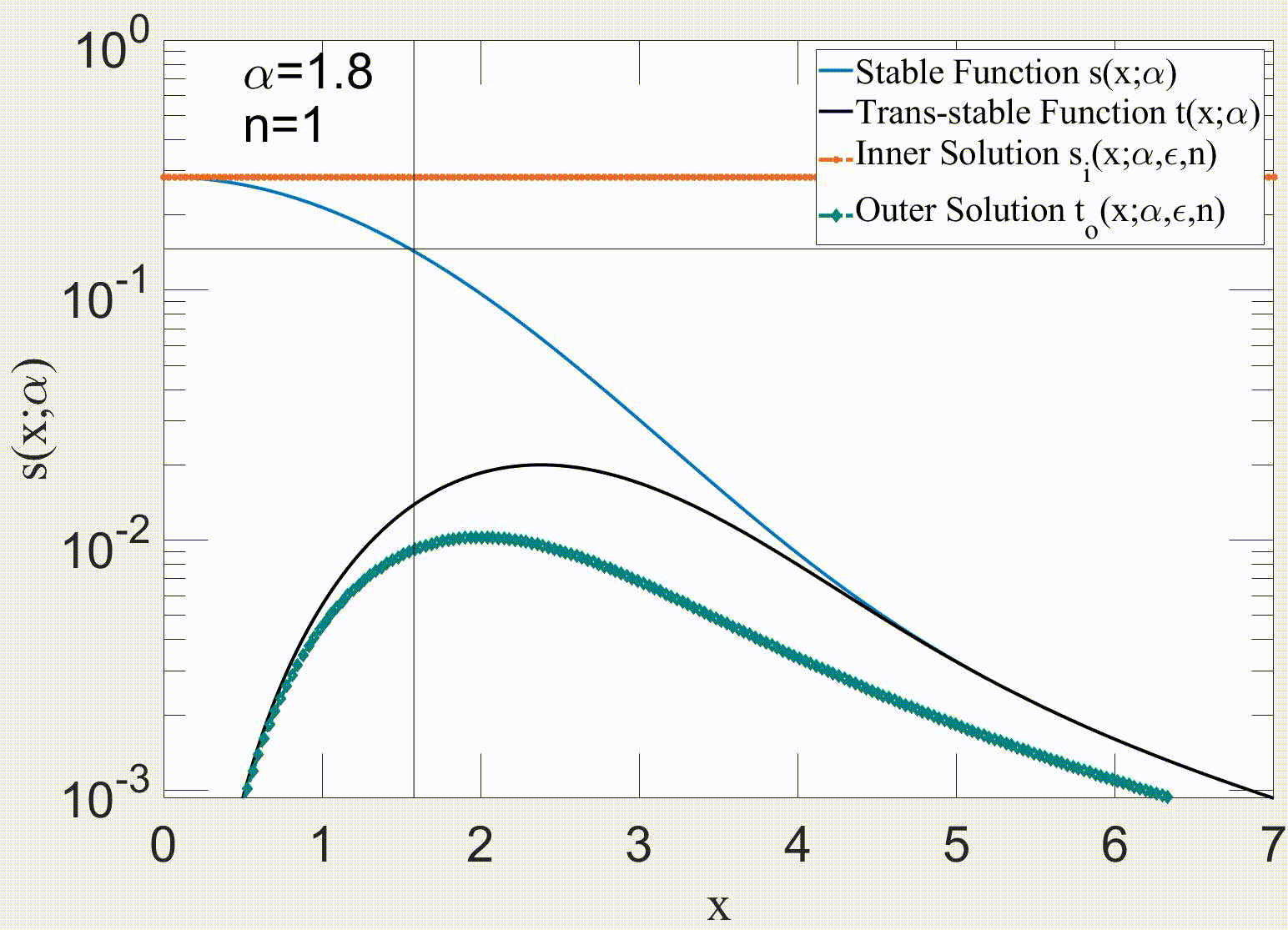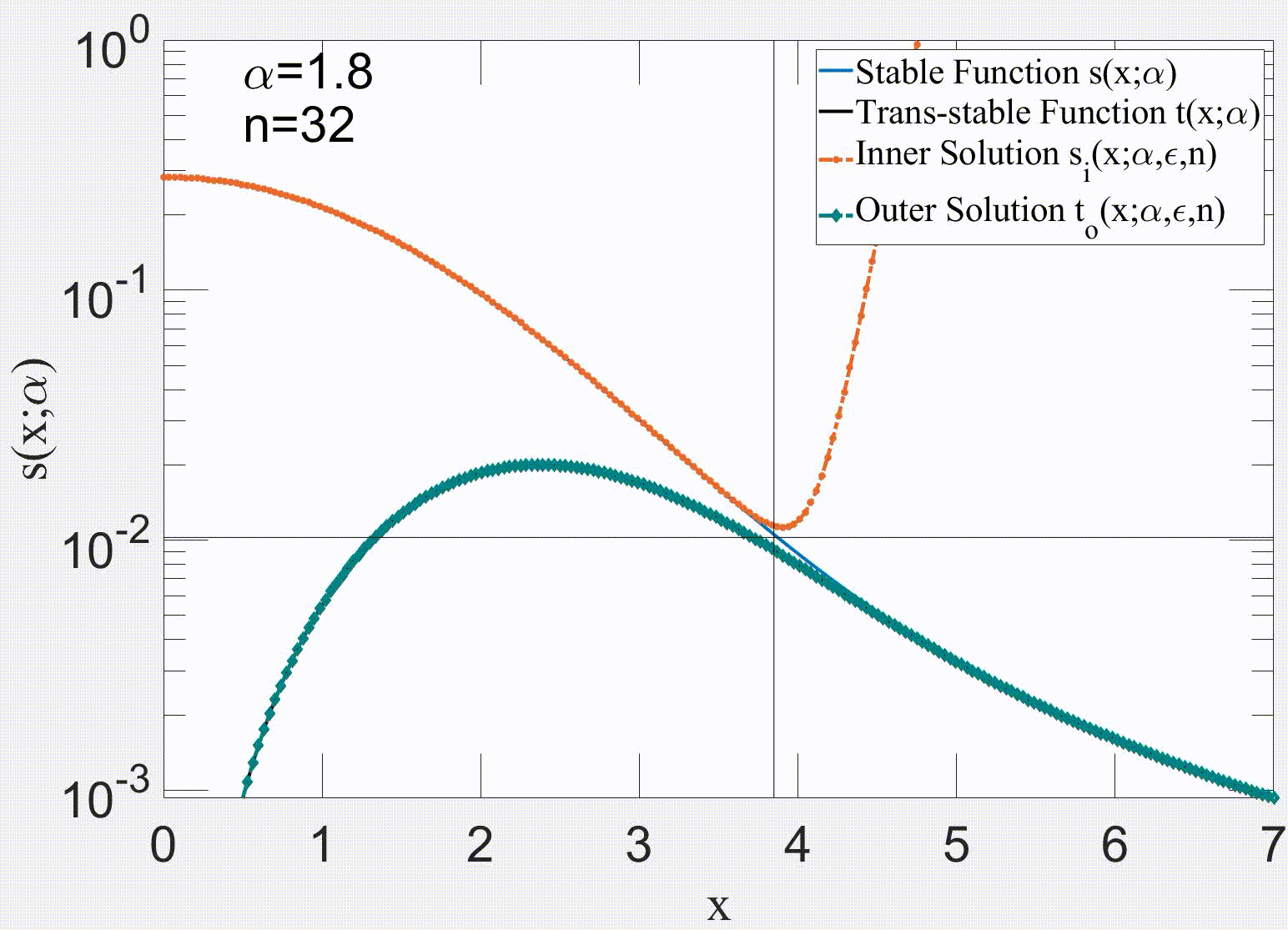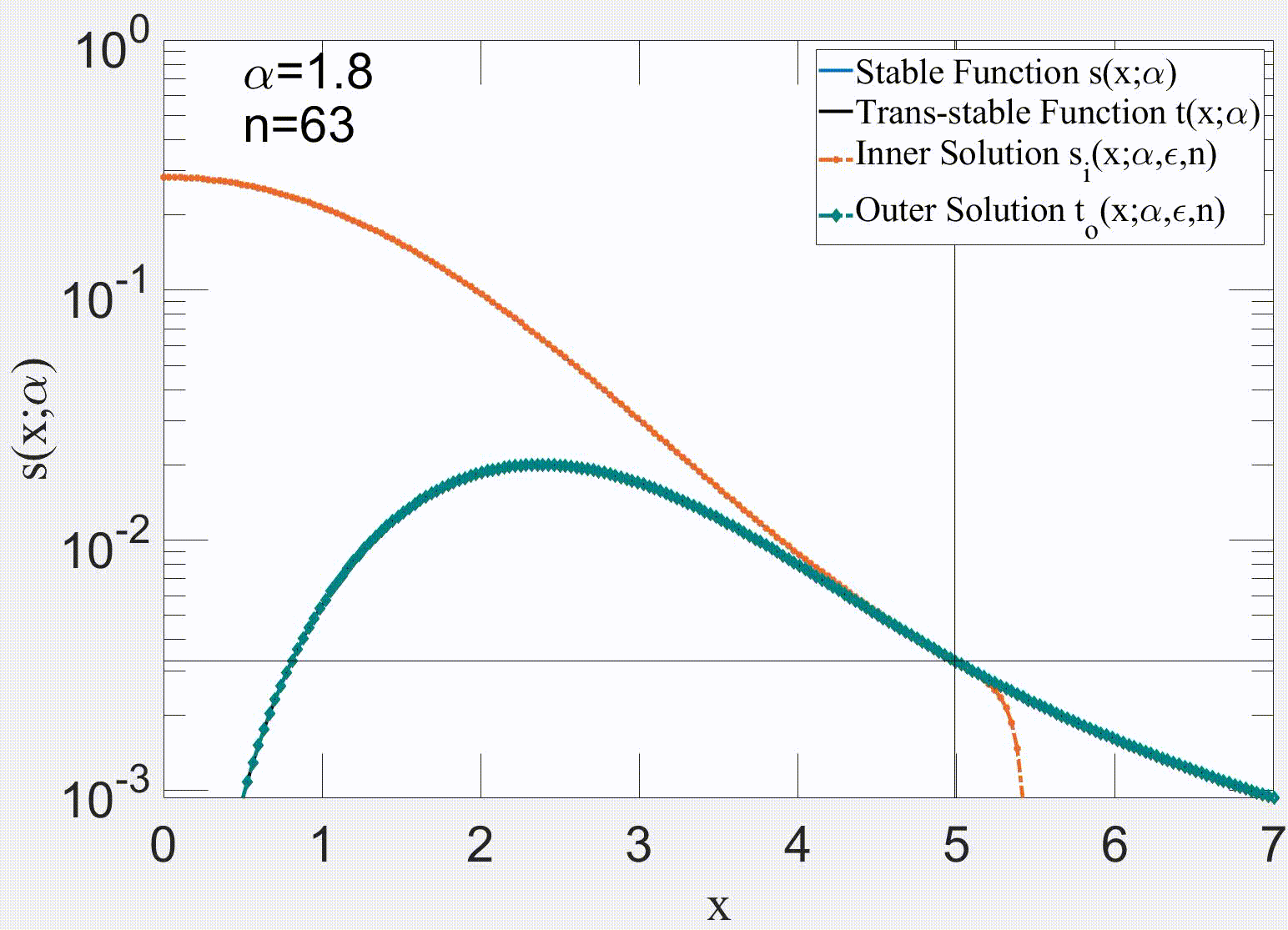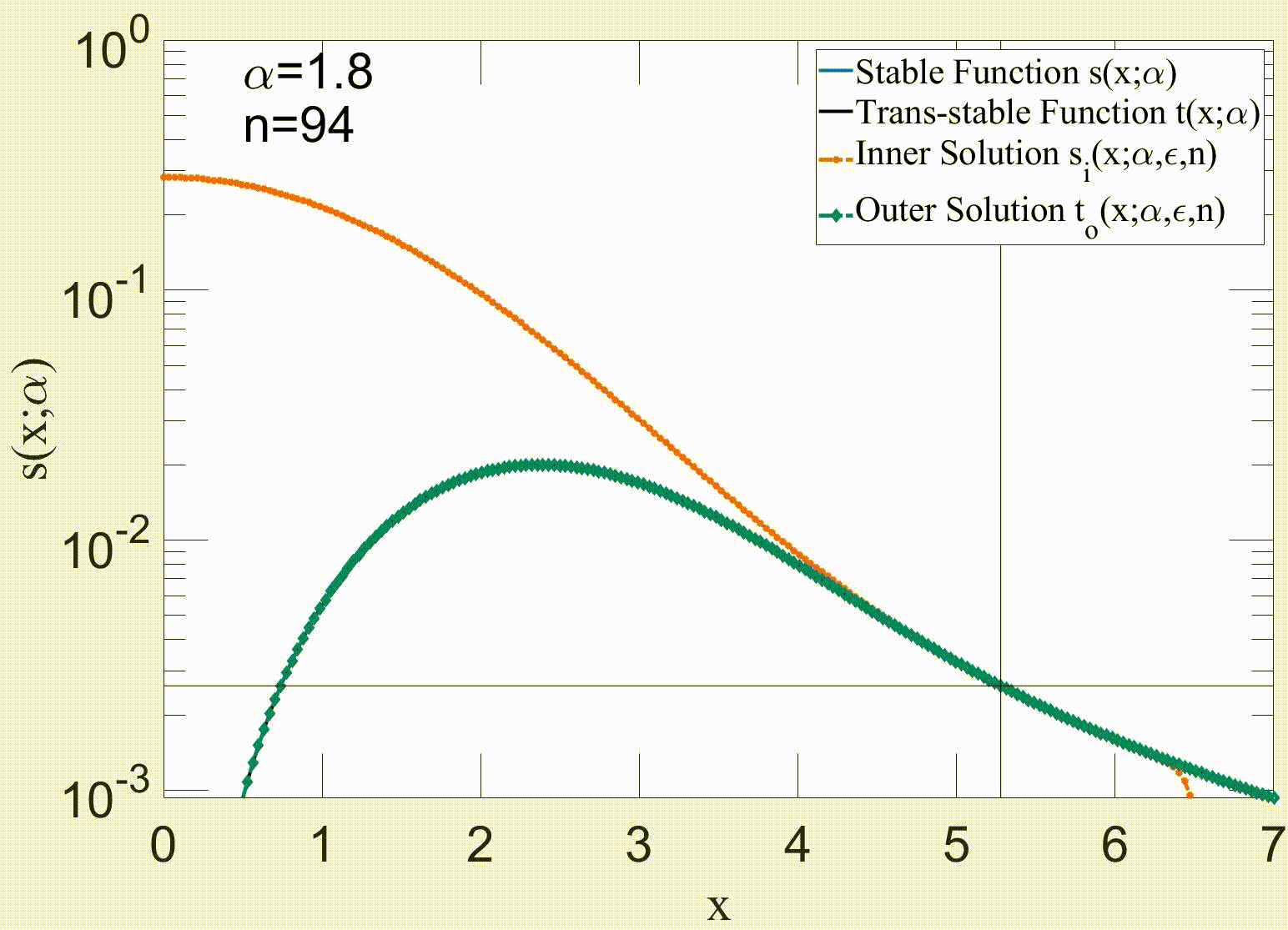
Our paper makes substantial advances in the analysis of the governing equation of the price return, which yields a new stochastic differential equation (SDE) that tries to cover limitations of Black-Scholes equation (BSE) and its modified versions. Our approach is to decompose the price return into a deterministic component, and stationary q-Gaussian noise. The deterministic term is associated with the systematic risk response to external events that can produce a change in the trend direction. Consequently, our proposed trend is smoother because it depends on the past values of the index. The detrended part is stationary and can be modelled by a q-Gaussian noise. Additionally, this manuscript presents various alternatives for evaluating the stationarity of the detrended price return. Some applied methods include examining the Hurst exponent and the power spectrum of the time series. In general, this paper proposes a methodology to decompose the price return, which can be applied to any index with available historical records for data analysis.

2021 Space-time fractional porous media equation: Application on modeling of S&P500 price return

Link: (click here)

In this paper, we present the generalized form of the PME (GPME) as a more accurate governing equation for modeling the detrended price return. The GPME admits fractional-order derivatives and allows us to have a derivative with respect to a function. The difference between GPME and the classic porous media equation (CPME) lies in the number and form of the fitting parameters, where the GPME allows us to obtain better fittings of stock market indexes. A particular solution of the GPME is the Green function, which can be expressed in terms of the Lq-Gaussian (first generalized q-Gaussian) and NLq-Gaussian functions (second generalized q-Gaussian). These functions were built by considering the local (LL) and non-local (NN) fractional derivative operators, respectively. The main finding is that the Lq-Gaussian and NLq-Gaussian functions admit generalized q-Gaussian functions that obey the self-similar law. These are characteristic features of price returns in stock markets. We present an analysis of the S&P500 as a case study, where the Lq-Gaussian and NLq-Gaussian have been used to model the detrended price return for the past 24 years (1996-2020). The Lq-Gaussian and NLq-Gaussian functions describe the probability density function (PDF) of the detrended price return well. The NLq-Gaussian is the best model for fitting the probability of the detrended price return.

2021 Methods for forecasting the effect of exogenous risks on stock markets

(click here)

Our paper presents insights into a critical outstanding problem in finding how the market is coupled to the natural environment, where an exogenous market shock is totally unpredictable and not initiated by any market-related events to produce a deterministic trend. The solution is that this trend is intimately related to the response of the natural environment to this shock without lag. Our highlighted case corresponds to model how the S&P500 responds to the coronavirus outbreak (COVID-19) based on the inflection points of the cumulative number of deaths and confirmed cases on the daily World Health Organization reports. The method was applied to construct a forecast of the S&P500 and provides an overview of the impacts of an exogenous market shock. This can be used as a reference to improve models' accuracy, which is of general interest and will have a far-reaching impact on cross-disciplinary research.

2019 Q-Gaussian diffusion in stock markets

(click here)

In this manuscript, we analyse the Standard & Poor’s 500 stock market of 22 years from 1996 to 2018 data per minute. We obtain a governing equation of price returns by deriving the porous media equation which models the empirical probability distributions of price return. Also, an explicit form for the diffusion coefficient of price changes for different times interval is proposed. The proposed function is very precise because it captures the full anatomy of the price return and is valid for other indexes as well. Our approach has a different focus on the solution of the porous media equation that preserves the self-similarity and central limit theorem concepts finding the limit of collapses for process with correlated random variables, and hence expanding the range of applicability of the porous media equation.

2018 Closed-form solutions for the Lévy-stable distribution

(click here)

In this manuscript, we derive a uniform analytical approximation for the stable (Levy) distribution function. This distribution results from the generalization of the central limit theorem for non-Gaussian processes. As presented in the introduction of our paper, these processes are very common in complex systems, but there are no robust analytical expressions for the statistics of their limited behaviour. Previous publications highlight the relevance of stable (Levy) processes in physics and the economy and propose solutions based on the truncation of the stable distribution. These truncations make the process become Gaussian in the asymptotic limit, which is not the case in some phenomena, such as the evolution of the price of the stock market indexes. Our approach presents a different paradigm of truncation that preserves the stable distribution as the asymptotic limit and hence expands the range of applicability of stable processes.