normal form theory

Normal form theory attempts to rigorously answer the question: when are two local representations actually just different representations of the same mathematical object? Moreover, it gives a procedure for computing the simplest representation of that object.

It is predominantly studied in the context of singularities (or fixed points) of vector fields and maps. In this context, a core question it answers is whether there exists smooth coordinates that transforms a nonlinear differential equation into its linearisation at a singularity.

Normal form theory for degenerate singularities of vector fields featured heavily in my thesis on collision singularities in the $n$-body problem. Using a geometric method called blow-up, the degenerate singularities were transformed into a normally hyperbolic manifold of non-degenerate singularities. Some mild adaptions of the usual normal form theory to this manifold of hyperbolic singularities provided a way to investigate orbits of the $n$-body problem close to collision. Ultimately, this resolved a conjecture about the nature of these near collision orbits. See (Duignan, 2019; Duignan & Dullin, 2020; Duignan & Dullin, 2021) for more details on the application to celestial mehanics, see (Duignan & Dullin, 2019) for details about blow-up in the plane, and see (Duignan, 2021) for normal form theory for normally hyperbolic invariant manifolds.

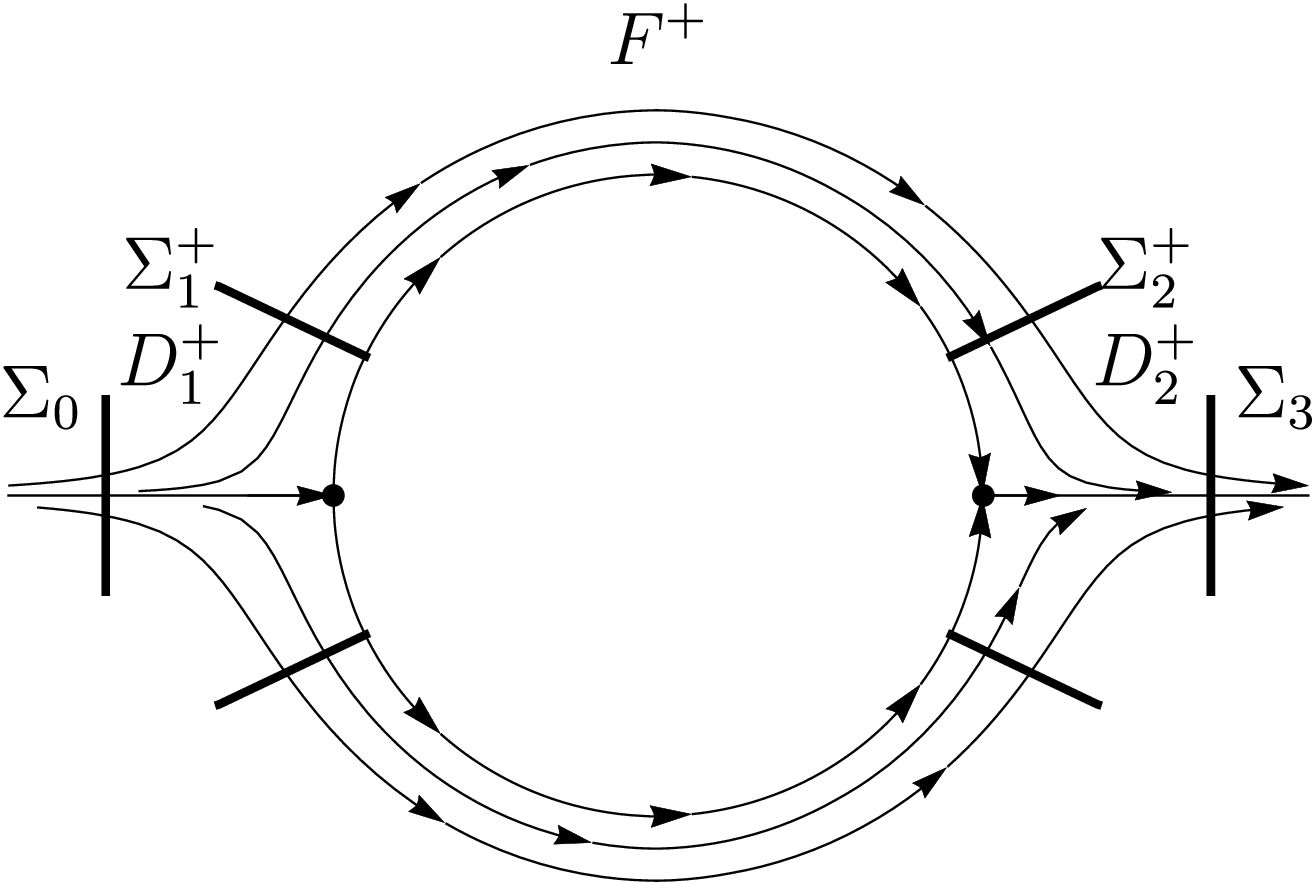
Most recently, myself, along with collaborators, have shown the connection between near-axis expansions of stellarator fields and normal form theory for Hamiltonian systems (see (Duignan & Meiss, 2021)). Moreover, the theory has proved useful in showing the existence of the much used Hamada and Boozer coordinates when in the neighbourhood of a magnetic axis. This work used many interesting ideas from presymplectic and symplectic geometry, see (Burby et al., 2021; Perrella et al., 2023).